Figure 1: Sorting Strings in Java
This work was supported by NSF grants CAREER 9702550 and CRCD 0088078.
Categories and Subject Descriptors K.3.2 [Computers & Education]: Computer & Information Science Education - Computer Science Education
General Terms Algorithms, Measurement, Theory
Keywords Analysis, Performance, Bubble sort
What do students remember from their first programming courses after one, five, and ten years? Most students will take only a few memories of what they have studied. As teachers of these students we should ensure that what they remember will serve them well. More specifically, if students take only a few memories about sorting from a first course what do we want these memories to be? Should the phrase Bubble Sort be the first that springs to mind at the end of a course or several years later? There are compelling reasons for excluding discussion of bubble sort2, but many texts continue to include discussion of the algorithm after years of warnings from scientists and educators. For example, in a popular new breadth-first text [6] bubble sort is given equal footing with selection sort and quicksort in online student exercises.
Starting with Knuth's premise that ``bubble sort seems to have nothing to recommend it''[17], we trace the origins and continued popularity of the algorithm from its earliest days as an unnamed sort to its current status as perhaps the most popular O(n2) sort (see below) despite wide-spread ridicule. We began this study with the intent to document (and ridicule) the continued popularity of bubble sort, but the algorithmic archaeological investigation has proven more interesting than casting aspersions.
Our initial premise that bubble sort should not be studied is reflected in [23] with a warning for potential misuse.
For N < 50, roughly, the method of straight insertion is concise and fast enough. We include it with some trepidation: it is an N2 algorithm, whose potential for misuse (by using it for too large an N) is great. The resultant waste of computer time is so awesome, that we were tempted not to include any N2 routine at all. We will draw the line, however, at the inefficient N2 algorithm bubble sort. If you know what bubble sort is, wipe it from your mind; if you don't know, make a point of never finding out!
This sentiment is similar to the reference to bubble sort found in [1], where it says of bogo sort, ``The archetypical perversely awful algorithm (as opposed to bubble sort, which is merely the generic bad algorithm).''
In Section 2 we trace the origin of the algorithm, both in name and in code. In Section 3 we analyze the performance of the algorithm and the simplicity of the code. In Section 4 we summarize our study.
In an effort to determine why bubble sort is popular we traced its origins. Knuth [17] does not provide information on the origin of the name, though he does provide a 1956 reference [10] to an analysis of the algorithm. That paper refers to ``sorting by exchange'', but not to bubble sort. An extensive bibliography and sequence of articles from the 1962 ACM Conference on Sorting [11] do not use the term bubble sort, although the ``sorting by exchange'' algorithm is mentioned. With no obvious definitive origin of the name ``bubble sort'', we investigated its origins by consulting early journal articles as well as professional and pedagogical texts.
An early (1959) book on programming [21] devotes a chapter to sorting, but uses the term exchange sorting rather than bubble sort. The same term is used in a 1962 [4] JACM article as well as in the earlier (1961, submitted 1959) [9] JACM article referenced as the definitive source. Iverson uses the name ``bubble sort'' in 1962 [13]; this appears to be the first use of the term in print. As we note below, each work cited in [13] uses a phrase other than ``bubble sort'' to describe the algorithm we describe in Section 2.1. This reinforces the claim that Iverson is the first to use the term, though obviously not conclusively. However, we could find no work published after 1962 with a reference to bubble sort in an earlier publication than Iverson's.
Despite these earlier publications the algorithm officially enters the ACM algorithm repository as Algorithm 175 [25] in 1963 where it is named Shuttle Sort. Soon thereafter [14] the published algorithm is found to be ``not free from errors'', a gentle way of saying the published code is wrong. There a modified version of the code (that stops early when no swaps are made) is given and the author says that in this form the code was ``studied in this form on the ORDVAC computer, Aberdeen Proving Ground, in 1955.''
Taking the description of bubble sort in [17] as definitive the code below is bubble sort.3 This version ``bubbles'' the largest elements to the end of the vector.
void BubbleSort(Vector a, int n)
{
for(int j=n-1; j > 0; j--)
for(int k=0; k < j; k++)
if (a[k+1] < a[k])
Swap(a,k,k+1);
}
Nearly every description of bubble sort describes how to
terminate the sort early if the vector becomes sorted.
This optimization requires checking if any swaps are made and
terminating if no swaps are made after j iterations of the inner
loop.
Another optimization is to alternate the direction of bubbling each time the inner loop iterates. This is shaker sort or cocktail shaker sort (see, e.g., [17,13]).
Nomenclature is interesting. An early (1963) Fortran textbook [22] refers to the following code as ``jump-down'' sort.
void JumpDownSort(Vector a, int n)
{
for(int j=n-1; j > 0; j--)
for(int k=0; k < j; k++)
if (a[j] < a[k])
Swap(a,k,j);
}
Bubble sort as we've identified it is called a ``push-down'' sort.
In another early (1962) work [19] the ``jump-down'' version
is presented first in the book, with no name. The bubble
sort follows also with no name. In two early works [3,10]
the jump-down sort is referred to as selection sort. Bubble sort is also
covered, but referred to as sorting by repeated comparison and
exchanging, respectively. In the latter paper, one of the
earliest works comparing algorithms, the exchange/bubble sort is
described thus: ``Exchanging requires at least twice as many
non-housekeeping comparisons as Inserting and for most computers will be
inferior''.
In moving from bubble sort to jump-down sort the only change to the code above is that one array index has been changed from k+1 to j. How does this differ from bubble sort? After m iterations of the outer loop the last m elements are in their final position-the same invariant as bubble sort. However, items are not ``bubbled'' to the top; this code implements what is essentially a selection sort, but the current maximal element is stored/swapped into location a[j] on each pass. We see why early works sometimes refer to jump-down as selection sort.
In a survey article on sorting appearing in 1971 [20] the first sort discussed is bubble sort. It is endorsed with the following qualities.
However, the bubble sort is easy to remember and to program, and little time is required to complete a single step.
As mentioned above, Knuth [17] belittles bubble sort. The first edition of this book appeared in 1973, but perhaps did not have the same influence as did early textbooks of the same period.4
In [2] (arguably the first ``real'' textbook on algorithms and algorithm analysis) we find the following endorsement.
However, we assume that the number of items to be sorted is moderately large. If one is going to sort only a handful of items, a simple strategy such as the O(n2) ``bubble sort'' is far more expedient.
Perhaps a generation of computer scientists and teachers used this book and the acceptability of bubble sort began. In the influential 1976 work Software Tools [15] the first sort mentioned is bubble sort (the second is Shell sort).
Why is bubble sort popular? In [26] we get an endorsement.
... Nevertheless, this sorting algorithm is commonly used where the value of n is not too large and programming effort is to be kept to a minimum. ... The bubble sort has the additional virtue that it requires almost no space in addition to that used to contain the input vector.
Perhaps early concerns with allocating registers and using memory led to the adoption of bubble sort which in its primitive form (no early stopping) requires no storage other than the array and two index variables. This conclusion is supported by the early explanations of selection sort (e.g., [3,]) in which only the version described in Section 2.1 as ``jump-down'' sort is described, no separate minimum index variable is kept, and the minimal element selected in each pass of selection sort is replaced by ``a series of 9's ... so that said item will never again be selected.'' [10].
Another early work [7] is referenced in [18] with the following warning.
From a mathematical standpoint, Demuth's thesis was a beautiful piece of work. ... But from a practical standpoint, the thesis was of no help. In fact, one of Demuth's main results was that in a certain sense ``bubble sorting'' is the optimum way to sort. ... It turns out that [all other sorting methods studied] are always better in practice, in spite of the fact that Demuth has proved the optimality of bubble sorting on a certain peculiar type of machine.
Demuth's work was published 29 years after he wrote it, and he does not recall using the term ``bubble sort'' in his studies. [8].
A 1988 SIGCSE paper [16] notes that bubble sort ``while once the best known sort, seems relegated to the status of an example of inefficiency''. Fifteen years later this sort is still with us, and students continue to use it.
Bubble sort is covered in many texts, occasionally as the only O(n2) sort, but often compared to another sort like insertion or selection. Rarely are its bad features emphasized. This may lead students to think that bubble sort is acceptable when it has provably bad performance and is arguably not the simplest sort to learn.
As unscientific albeit interesting evidence of popularity, on August 1, 2000 we searched the Internet for different sorts using the search engine Google. We repeated this search in August of 2002. For each method we used the name with and without a space, e.g., ``bubblesort'' and ``bubble sort''. Table 1 shows the results.
| sort | # hits 2000 | # hits 2002 |
| Quick | 26,780 | 80,200 |
| Merge | 13,330 | 33,500 |
| Heap | 9,830 | 22,960 |
| Bubble | 12,400 | 33,800 |
| Insertion | 8,450 | 21,870 |
| Selection | 6,720 | 20,600 |
| Shell | 4,540 | 8,620 |
The good news is that Quicksort is by far the most-referenced sort on the web. The bad news is that bubble sort is the second or third most popular sort and is by far the most cited O(n2) sort.5 Hopefully the situation is somewhat mitigated by the greater rate of increase in hits for selection sort compared to bubble sort.
Here we show that by several measures bubble sort is not simpler to code than other sorts and that its performance is terrible. We worry about bubble sort because of its inexplicable popularity. We view the use of bubble sort as an instance of a larger problem: choosing examples that are not exemplars of accepted best-practices. Such examples invariably must be unlearned later which is often an impossible task.
Conventional wisdom holds that bubble sort is simple to program. For example, in [5] we find: ``The bubble sort is worse than selection sort for a jumbled array-it will require many more component exchanges-but it's just as good as insertion sort for a pretty well-ordered array. More important, it's usually the easiest one to write correctly.''
However, in [24] we find a weak rebuttal.
Bubble sort's prime virtue is that it is easy to implement, but whether it is actually easier to implement than insertion or selection sort is arguable.
This rebuttal is stated more forcefully in [27].
The bubble sort algorithm is not very useful in practice, since it runs more slowly than insertion sort and selection sort, yet is more complicated to program.
Software metrics are controversial. However, perhaps the most-cited metrics based on a static analysis of code (no control-flow paths) are the Halstead Metrics [12]. These metrics are based on counts of operators and operands, though symbols such as a semi-colon are interpreted as operators. Table 2 gives the Difficulty and Effort measures for several sorts.6
Difficulty purports to measure how hard it is to create the program. Effort purports to measure the effort required to convert an algorithm into a program.
| sort | D | E |
| Bubble | 17.25 | 4165 |
| Jump-down | 14.38 | 3828 |
| Select | 15.95 | 4242 |
| Insert | 23.20 | 6652 |
| Quick | 7.88 | 3157 |
| Partition | 12.07 | 1522 |
For some perspective on these numbers consider an implementation of selection divided into two parts: a function to return the index of the minimal element and the sorting function below.
void SelectSort(Vector a, int n)
{
for(int j=0; j< n-1;j++) {
Swap(a, minIndex(a,j,n), j);
}
}
This version of selection sort has a difficulty of 7.88 and an effort of 966; the minimal index function has D=14 and E=2247.
Note that the implementation of quick sort is divided into two functions, one recursive (Quick in Table 2) and one with a single loop (Partition).
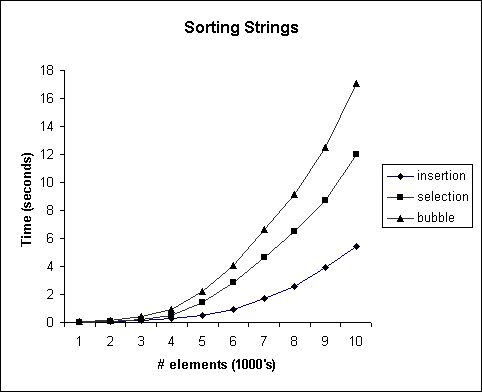
Although popular, bubble sort is nearly universally derided for its poor performance on random data. This derision is justified as shown in Figure 1 where bubble sort is nearly three times as slow as insertion sort.

Figure 1: Sorting Strings in Java
Some books laud bubble sort because it runs in O(n) time on sorted data and works well on ``nearly sorted'' data. In [24] this is qualified in slightly more detail with the conclusion that insertion sort is better than bubble sort, is stable, and is the basis for the more efficient Shell sort.
This leaves little to recommend bubble sort. In any situation in which it does well insertion sort does as well and is better by other criteria. Insertion sort is used to sort small (sub) arrays in standard Java and C++ libraries.
In most practical situations the best sort to use is the one provided by the standard (e.g., Java, C, or C++) libraries. However, we study sorts because general sorts do not work in all situations and because sorting is a simple illustration of algorithmic techniques. Although examples used in first year courses must be simple enough to be understandable and complex enough to be useful in a variety of situations, they should also exemplify best practices so that these practices endure after many of the details of a course have been forgotten. In this paper we have investigated the origins of bubble sort and its enduring popularity despite warnings against its use by many experts. We confirm the warnings by analyzing its complexity both in coding and runtime.
2 A discussion of bubble sort with warnings that the performance is bad and the code isn't simple (arguably) is like telling someone ``don't think about pink elephants.''
3 This code is close to legal in both C++ and Java and should be readable by anyone with a working knowledge of Algol-like languages.
4 We are not arguing that Knuth's work is less substantial, but that it may have had less of a curricular impact than books specifically designed as textbooks rather than as works of reference.
5 It is possible though unlikely that every web page referring to bubble sorts extols its bad qualities.
6 These metrics were calculated automatically from the code given in this paper using a tool from and verified as accurate using the Unix program npath.